STRUKTUR IDE
Ide adalah sebuah pemikiran
seseorang untuk menghasilkan sesuatu yang baru. Entah itu berupa pendapat
maupun menghasilkan benda. Ide bisa dikombinasikan dengan pengalaman maupun
intuisi. Ide sangat dibutuhkan untuk memecahkan masalah apapun dalam kehidupan,
seperti pekerjaan, pendidikan, maupun masalah – masalah yang sederhana dalam
kehidupan sehari – hari.
Dengan adanya ide membuat kita
semakin kreatif, semakin berkembang dan pemikiran tidak hanya pada satu sudut
pandang. Kreatif bisa dihasilkan ketika setelah memperoleh pengalaman yang
kemudian disintesis.
Pikiran, ide
dan gagasan mempunyai wujud memori yang disimpan di otak. Wujud memori manusia
adalah selaput mielin yang membungkus akson neuron. dengan memori manusia bisa
mengingat, berpikir, bahkan membayangkan (berimajinasi). Ukuran pengetahuan
manusia secara fisik adalah tebal mielin itu sedangkan kecerdasan manusia dapat
diukur dengan banyak hubungan antara akson. jika hubungan antar neuron semakin
banyak, semakin cerdas manusia itu dan kreatif karena dapat menghubungkan
data-data dengan banyak cara. kecerdasan adalah ukuran kemampuan manusia dalam
menemukan jawaban suatu masalah dengan benar, cepat dan tepat.
Ada dua cara menympulkan
dalam pemikiran manusia. Secara induksi dan deduksi. Induksi adalah cara dalam
menyimpulkan dari hal-hal umum berdasarkan kesamaan antara data-data khusus.
Contohnya, kita mencoba rasa anggur dari 300 anggur selama setahun. kita
mendapatkan rasa manis. Maka kita menyimpulkan semua anggur itu rasanya manis.
Sedangkan deduksi adalah cara dalam menyimpulkan hal-hal khusus berdasarkan fakta umum. contoh: orang jawa berbahasa jawa. Dedi orang jawa maka Dedi bisa berbahasa jawa.
Sedangkan deduksi adalah cara dalam menyimpulkan hal-hal khusus berdasarkan fakta umum. contoh: orang jawa berbahasa jawa. Dedi orang jawa maka Dedi bisa berbahasa jawa.
Kegiatan pemikiran ini
menggunakan logika sehingga melahirkan ilmu logika. ilmu logika yaitu ilmu yang
membahasa cara berpikir yang benar sehingga didapat hasil yang benar, masuk
akal dan dianggap benar. Ide atau gagasan yang tersusun dalam pikiran kita
dapat muncul di mana saja dan dipicu oleh apa saja yang ada di sekitar kita.
Ide itu bisa muncul dari kehidupan kita, saat sedang membaca buku atau koran di
pagi hari, bahkan bisa juga saat kita sedang melihat pertandingan olahraga.
Pandangan awal tentang ide
pertama kali diungkapkan oleh Plato pada zaman Yunani kuno sekitar abad 427 SM
hingga 347 SM. Menurut Plato, ide tidak diciptakan oleh pemikiran manusia. Ide tidak tergantung pada pemikiran manusia, melainkan
pikiran manusia yang tergantung pada ide.
Ide bawaan, dalam filsafat,
gagasan diduga bawaan dalam pikiran manusia, sebagai sesutu yang berbeda dengan
yang diterima atau dikompilasi dari pengalaman. Doktrin bahwa ide-ide
setidaknya tertentu (misalnya, orang-orang dari Allah, ketidakterbatasan,
substansi) harus bawaan, karena tidak ada asal empiris bagi mereka bisa
dipahami, berkembang di abad ke-17 dan ditemukan di Rene Descartes merupakan
kritik yang cukup terkenal. Teori ini memiliki macam-macam bentuk. Beberapa
menyatakan bahwa anak yang baru lahir memiliki kesadaran eksplisit, ide di
dalamnya. Orang lain, lebih umum, menyatakan bahwa ide-ide bawaan memiliki
beberapa bentuk implisit, baik sebagai kecenderungan atau sebagai kapasitas
aktif untuk perubahan mereka, beberapa kasus membutuhkan pengalaman yang baik
bagi perkembangan mereka.
Esensi atau sifat pikiran,
Descartes mengatakan itu adalah berpikir. Jika hal tidak berpikir, tidak
pikiran. Dalam hal ontologi nya, pikiran adalah zat (terbatas), dan berpikir
atau berpikir adalah atribut. Sejauh esensi atau sifat pikiran adalah berpikir,
di mana pikiran adalah fitur pikiran mendefinisikan, Descartes menyebutnya
atribut pokok pikiran.
Kritik yang lain oleh John
Locke kemudian di abad itu ditujukan terhadap prinsip-prinsip bawaan (aksioma yang
seharusnya, baik teoritis dan praktis, ditanamkan dalam pikiran oleh alam) dan
ide-ide bawaan diklaim sebagai hal prinsip. Tapi empirisme Locke memiliki
kesulitan dengan konsep-konsep penting, seperti substansi, "Yang tidak
kita miliki juga tidak bisa memiliki dengan sensasi atau refleksi,"
tentang yang ia sebagian besar mengantisipasi kesulitan David Hume pada abad
ke-18. Locke tampaknya telah berbagi beberapa asumsi dari lawan-lawannya
(misalnya, bahwa jika ide bawaan tidak bisa salah) dan telah merasakan bahwa
itu salah satu logika (status dari proposisi apriori) dan bukan dari genetik psikologi.
Masih dalam perbedaan ini,
abad ke-18 filsuf Immanuel Kant telah mengganti doktrin ide-ide bawaan dengan
pertanyaan tentang konsep priori, yang dicirikan bukan dari aslanya tetapi
kebutuhan mereka menganggap sebagai kondisi pengalaman manusia dari dunia
objektif. Pada abad ke-20, Noam Chomsky seorang profesor linguistik berpendapat
perlunya untuk mendalilkan ide-ide bawaan untuk menjelaskan ke bentuk bahasa.
Saat ini, ide untuk
memecahkan masalah banyak sekali seperti pekerjaan maupun dalam masalah
keuangan. Ide saat ini bisa dijadikan ladang bisnis. Seperti sekarang ini, ide
– ide yang sudah menjamur yaitu bisnis dengan memanfaatkan internet, Sehingga
berbisnis dengan mencantummkan gambar dan harga yang ditawarkan. Namun adapun
kekurangan dalam ide ini, yaitu calon pembeli tidak dapat melihat langsung
barang yang dijualkan. Ide – ide orang kreatif juga banyak menghasilkan produk
berupa teknologi canggih seperti handphone yang sekarang harganya sudah
bisa dijangkau masyarakat dari segala lapisan.
Dalam dunia pendidikan, ide
juga dapat direalisasikan dengan mempraktekkannya di depan siswa atau
mahasiswa. Ide dalam pendidikan ini berupa cara atau metode dalam menyampaikan
ilmu kepada siswa maupun mahasiswanya agar siswanya mengerti apa yang
disampaikan oleh pendidiknya. Selain itu, ide dari peserta didik juga bisa
direalisasikan dengan bagaimana cara siswa menyelesaikan pertanyaan –
pertanyaan yang disediakan oleh pendidiknya. Dengan berbagai macam cara
merupakan suatu ide dalam menyelesaikan masalah.
Ide yang
sudah dinyatakan menjadi suatu perbuatan adalah karya cipta. Untuk mengubah ide menjadi karya cipta dilakukan
serangkaian proses berpikir yang logis dan seringkali realisasinya memerlukan
usaha yang terus menerus sehingga antara ide
awal yang muncul di pikiran dan
karya cipta satu sama lain saling bersesuaian sebagai kenyataan. Alam pikiran
(dalam Yunani) yang menjangkau pengertian Ide Ideal atau Ide
Sempurna. Aliran yang telah kita ketahui yaitu aliran filsafat Idealisme. Dari
pemikiran tentang yang sempurna itu lahirlah gagasan-gagaan tentang ketuhanan
sebagai Ide Ideal tertinggi yang dapat dipikirkan dan dirasakan oleh
manusia keberadaannya yaitu tentang Pencipta Makhluk atau Tuhan.
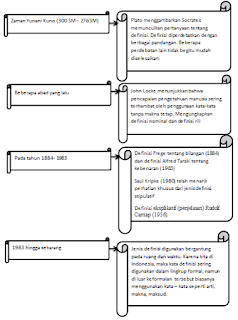
Gambar 1. Bagan yang digambar dari
ulasan struktur ide
DAFTAR PUSTAKA
STRUKTUR IDE
Disusun Guna Memenuhi Tugas Mata Kuliah Matematika
Model
Dosen Pengampu: Prof. Dr. Marsigit, M.A

Disusun oleh:
Diana Amirotuz Zuraida (15709251066)
(dianaamirotuz.blogspot.com)
PROGRAM STUDI
PENDIDIKAN MATEMATIKA
PROGRAM PASCASARJANA
UNIVERSITAS NEGERI
YOGYAKARTA
2016
 |